<== HALL CHARTREUSE
Informatique
<== HALL BELLEDONNE
Science et techniques
<== Hall du parcours
« Les composants »
Binaire et fonctions logiques
ET - OU - NON
Au coeur de la machine on trouve des « circuits logiques ».
Ce sont les circuits qui traitent les signaux binaires : des signaux qui ne connaissent que 2 états vrai ou faux, oui ou non, +5V ou 0V, 1 ou 0 !
Pourquoi se contenter de 2 états 0 et 1, et ne pas utiliser les 10 chiffres de notre numération habituelle ?
Parce qu'en électronique il est facile de distinguer 2 états :
- le courant passe /le courant ne passe pas...
- le signal est plus grand que 2,5 V / le signal est plus petit que 2,5 V...
Alors que créer des circuits qui distingueraient (et feraient des opérations) sur des valeurs 0,5V, 1V, 1,5V, 2V, 2,5V... serait difficile : couteux en matériel et lent à l'exécution.
Notes :
- Une variante de ce parcours expliquera bientôt le détail technique des circuits présentés ici.
- Les « calculateurs analogiques » des années 1950 utilisaient directement la mesure des courants électriques, mais ce n'était pas des ordinateurs. Nous ferons un parcours spécial sur ces superbes machines.
Un mathématicien, George Boole (1815-1864) a longuement étudié la logique mathématique et a établi une « algèbre » binaire pour les éléments à 2 états.
Il existe trois fonctions de base :
- ET : la fonction donne un "1" si toutes les entrées sont à "1"
- OU : la fonction donne un "1" si au moins l'une des entrées est à "1"
- NON : la fonction donne un "1" si l'entrée est à "0"
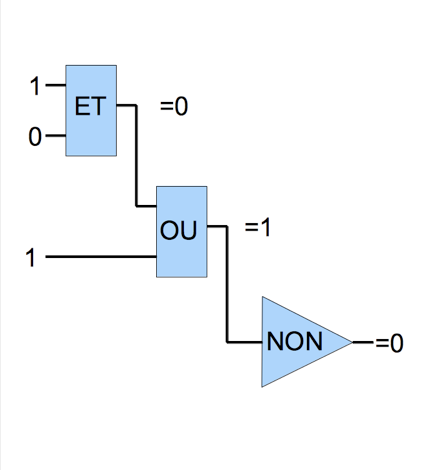
Sur le dessin ci-contre, l'élément "ET" en haut donne "0" car une des entrées est restée à 0.
Par contre l'élement "OU" en dessous donne un "1" car l'une des entrées est à 1.
Enfin l'élement "NON" en bas qui reçoit un "1" sort l'inverse, soit "0".
Et toute la logique de nos ordinateurs va être entièrement conçue sur ces 3 fonctions de base !
La "bascule" mémoire
Voici un exemple, très important, de la puissance de ces fonctions, car elle va nous permettre de mémoriser la valeur d'un élément binaire (un "bit") entre deux opérations.
Deux éléments "NON" couplés ensemble se "verrouillent" l'un l'autre :
- Si l'un sort "1" l'autre sort "0"
- et le système est stable.
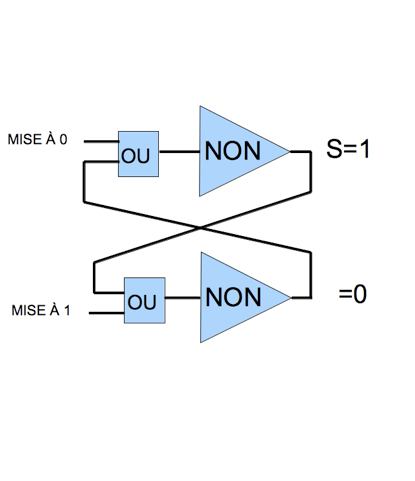
Notez les deux fonctions "OU" ajoutées sur les entrées dans le dessin ci-contre : ils vont nous permettre de commander le changement d'état :
- la bascule est ici dans l'état "1", les deux entrées "mise à 1" et "mise à 0" sont à l'état "0"
- si je place un "1" sur l'entrée "mise à 0", le circuit "OU" va donner "1" en sortie...
- le circuit "NON" supérieur va alors sortir un "0"
- le circuit "OU" du bas ne reçoit que des "0" et sort "0"
- le circuit "NON" du bas reçoit 0 et sort "1"
... ... et nous sommes dans un nouvel état stable, inverse du premier avec la sortie S=0.
Cet ensemble est couramment appelé "bascule" ou "flip-flop en anglais.